5 ejemplos de paradojas que te dejarán con la boca abierta
Paradoja se refiere a un hecho o una frase que parece oponerse a los principios de la lógica. Algunos ejemplos de paradojas famosas son las siguientes.

¿Qué es Paradoja? Paradoja se refiere a un hecho o una frase que parece oponerse a los principios de la lógica. La palabra proviene del latín paradoxa, plural de paradoxon, que significa ‘lo contrario a la opinión común’; este a su vez viene del griego παράδοξα (parádoxa), plural de παράδοξον (parádoxon), que podría traducirse como ‘inesperado’, ‘increíble’ o ‘singular’. Aquí te decimos algunas paradojas y sus ejemplos más famosos.
Algunos ejemplos de paradojas…
1. Paradoja de los gemelos

Esta teoría fue propuesta por Albert Einstein al desarrollar lo que hoy se conoce como la teoría de la relatividad especial.
Dicha paradoja expone que si tenemos a dos gemelos y a uno de ellos lo montamos en una nave espacial que alcanza velocidades cercanas a la velocidad de la luz y otro lo dejamos en la Tierra, cuando el que fue al espacio regrese, vería que es más joven que el que se ha quedado en la Tierra.
Dicha teoría postula que la medida del tiempo no es absoluta. Además, siendo dos observadores, el tiempo medido entre dos eventos por estos observadores, en general, no coincide. La diferente medida de tiempos depende del estado de movimiento relativo entre ellos.
2. Paradoja del abuelo

Se trata de las paradojas más famosas, y dice que si una persona realiza un viaje a través del tiempo y mata al padre biológico de su padre/madre biológico (abuelo del viajero), antes de que este conozca a la abuela del viajero y puedan concebir, el padre/madre del viajero (y por extensión, ese viajero) nunca habrá sido concebido, de tal manera que no habrá podido viajar en el tiempo.
Por otro lado, y continuando con la hipótesis, al no viajar al pasado, el abuelo del viajero no sería asesinado, por lo que el hipotético viajero sí es concebido; entonces, sí puede viajar al pasado y asesinar a su abuelo, pero no sería concebido, y así indefinidamente.
La paradoja surge porque el estado actual del mundo está determinado por sus estados anteriores, de manera que cambiar uno de estos estados propaga incontroladamente efectos hacia el estado actual.
3. Paradoja del gato de Schrödinger

El escenario presenta que puede estar simultáneamente vivo y muerto, un estado conocido como superposición cuántica, como resultado de estar vinculado a un evento subatómico aleatorio que puede ocurrir o no.
4. Paradoja de Möbius

Se trata de la cinta Möbius o Moebius, creada por el matemático y astrónomo alemán August Ferdinand Möbius en 1858. La paradoja de la cinta de Möbius es una paradoja visual de una cinta con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable.
Una de las características más fascinantes de la cinta de Moebius es que es lo que los matemáticos llaman un “objeto no orientable”.
“Es algo que intuitivamente es complicado de entender”, le dice a BBC Mundo Alejandro Adem, profesor de matemáticas en la Universidad de la Columbia Británica en Canadá.
5. Paradoja del hotel infinito
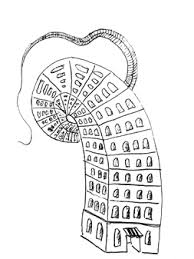
Esta paradoja dice que Imaginemos que queremos construir el hotel más grande del mundo. Al principio, pensamos en hacer uno de 1.000 habitaciones, pero es posible que alguien lo supere. Lo mismo pasa con 20.000, 500.000, 1.000.000…
El matemático alemán David Hilbert propuso el Hotel Infinito como una forma de explicar estas curiosas paradojas del infinito, explicando cómo serían las cosas en un hotel con infinitas habitaciones si llegara un huésped más cuando todas estas estuvieran ocupadas, si llegaran infinitos huéspedes, o incluso si llegara un infinito número de grupos infinitos de turistas.
Por ello, se llega a la conclusión de que lo mejor es construir uno con habitaciones infinitas. El problema radica que en un hotel infinito que se llena de infinitos huéspedes, las matemáticas nos dicen que se llenaría por completo. ¿Se puede llegar al infinito +1?